Histoire de la Numération Égyptienne

La Numération Égyptienne – et par extension les mathématiques – étaient utilisées pour mesurer le temps, les lignes droites, le niveau des crues du Nil, calculer les surfaces de terre, compter l’argent, calculer les impôts et cuisiner. La Numération Égyptienne était même utilisée dans la mythologie… Apprenez-en plus avec cet article !

Le système de Numération Égyptienne

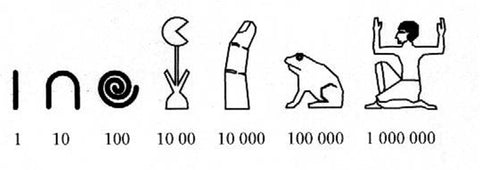
On pense que le premier système de Numération Égyptienne a été introduit et entièrement développé sur la base des décimales au moins dès 2.700 avant J.-C. – probablement même bien avant. Pour représenter les nombres à l’écrit, on utilisait sept symboles :

un bâton pour les unités,
une anse pour les dizaines,
une corde enroulée pour les centaines,
un lotus pour les milliers,
un index pour les dizaines de millier,
une grenouille (ou têtard) pour les centaines de millier,
un dieu pour le million (qui représentait également l’infini).

Avec le système de Numération Égyptienne, les mathématiques se développèrent. Une partie du plus grand parchemin mathématique qui subsiste, le Papyrus Rhind (écrit en caractères hiératiques), pose des questions sur la géométrie des triangles. Il s’agit, par essence, d’un manuel de mathématiques. Les parties du papyrus qui subsistent montrent comment les ingénieurs égyptiens calculaient les proportions des pyramides ainsi que d’autres structures. À l’origine, ce papyrus mesurait cinq mètres de long et trente-trois centimètres de haut.

Le système de Numération Égyptienne et l’origine des mathématiques

C’est dans la vallée du Nil que nous devons chercher les preuves de l’influence précoce des Égyptiens sur les mathématiques grecques. En ce qui concerne la géométrie, les égyptologues sont unanimes : les prêtres-mathématiciens de la vallée du Nil étaient les premiers. La géométrie de Pythagore, Eudoxus, Platon et Euclide a été apprise dans les temples de la vallée du Nil. Quatre papyrus mathématiques subsistent encore, dont le plus important est le papyrus mathématique de Rhind, datant d’environ 2.000 avant J.-C. Non seulement ces papyrus montrent que les prêtres maîtrisaient tous les processus de l’arithmétique, y compris une théorie des nombres, mais qu’ils avaient développé des formules leur permettant de trouver des solutions aux problèmes à une et deux inconnues, ainsi que des problèmes de « pensée d’un nombre ». Avec tout cela, plus les progressions arithmétiques et géométriques qu’ils ont découvertes, il est évident qu’en ce temps-là, l’algèbre était en place dans la vallée du Nil.

Le Papyrus Rhind livre une équation qui permet de trouver l’angle de la pente de la face d’une pyramide. En outre, on avait les moyens, avec les modèles pyramidaux, d’obtenir les valeurs du sinus et du cosinus. Ainsi, la trigonométrie a également été développée dans la vallée du Nil. L’état avancé de cette mathématique est confirmé par un dessin architectural encore plus ancien que le Papyrus Rhind, qui montre que les ingénieurs du Nil avaient appris à évaluer l’aire d’un cercle il y a plus de 5.000 ans. Enfin, comme l’a constaté Flinders Petrie, les architectes avaient plusieurs fois intégré dans leurs structures des triangles droits qui obéissaient au théorème : a2 + b2 = c2, où a et b sont les deux côtés et c l’hypoténuse. Pythagore ayant étudié dans les temples de la vallée du Nil pendant 22 ans, il n’aurait pas été surpris d’apprendre qu’il y avait là la source du théorème qui porte son nom.

Le Papyrus Rhind pose également des questions telles que « A partir d’une certaine quantité de grain, combien de pains peut-on cuire ? » ou « Étant donnée une rampe de longueur x et de hauteur y, combien de briques sont nécessaires à sa construction ? » Ce sont des exemples typiques de ce que les écoliers égyptiens devaient faire dans leur classe de mathématiques.

Les Égyptiens, avec leur système de Numération Égyptienne, connaissaient l’addition, la soustraction, une certaine division et la multiplication. Ils ne faisaient que multiplier et diviser par deux, donc s’ils voulaient trouver e x 5, ils utilisaient e x 2 + e x 2 + e. Autre exemple : 13 / 4 était calculé ainsi : 4 x 2 + 4 = 12, 13 – 12 = 1, et donc la réponse était donc 3.

Comme on ne savait multiplier ou diviser que par deux, les mathématiques égyptiennes étaient difficiles à manier. Pour obtenir des nombres entiers comme 32, les Égyptiens devaient écrire : 10 + 10 + 10 + 1 + 1. Bien que simple, le système de Numération Égyptienne, obligeait à une écriture complexe : un million ne nécessitait, certes, qu’un caractère ; mais un million moins un en nécessitait cinquante-quatre.

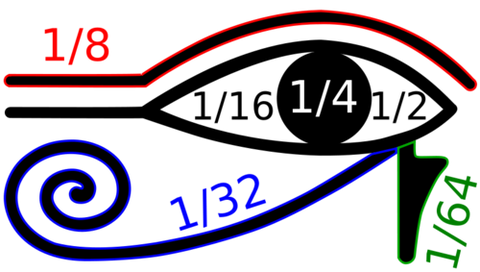
D’autres fractions pourraient être faites à partir de la représentation des différentes parties de l’œil d’Horus. Il a été divisé en 1/2, 1/4, 1/8, 1/16, 1/32 et 1/64. On trouve l’origine de l’emploi de l’œil d’Horus dans le mythe selon lequel Seth, l’oncle d’Horus, lui arracha son œil et le découpa en morceaux. Thot, plus tard, recomposa l’œil en joignant les parties ensemble.

Le système de Numération Égyptienne, cependant, ne comprenait pas de concept pour le chiffre zéro. Ce dernier fut inventé indépendamment par les Indiens et les Mayas. Les Indiens utilisaient un espace pour le zéro, et les Mayas utilisaient un symbole pour le zéro dans leurs calendriers, dès le 3^e siècle après J.-C. Les Indiens ont fini par utiliser un point pour le zéro, et celui-ci fut repris par les Arabes. Grâce aux Arabes, le chiffre zéro a atteint la civilisation européenne après 800 après J.-C. Les anciens Égyptiens, tout comme les Grecs et les Romains, n’avaient pas besoin du zéro.

Les applications des mathématiques et du système de Numération Égyptienne dans l’Égypte antique

Dans leur vie quotidienne, les Égyptiens qui utilisaient le plus le système de Numération Égyptienne les mathématiques étaient probablement les prêtres et les prêtresses en charge d’ouvriers, les géomètres, les maçons et les ingénieurs, les collecteurs d’impôts, les commerçants et au moins une partie des acheteurs, et des cuisiniers. La forme supérieure des mathématiques, bien sûr, était faite par ceux qui avaient des emplois liés au bâtiment et par les prêtres. Les commerçants, les cuisiniers et les classes inférieures n’utilisaient probablement que les types de mathématiques simples que nous utilisons aujourd’hui dans notre vie quotidienne.

Les Égyptiens calculaient le nombre de jours dans l’année avec leur calendrier. Ils étaient l’un des peuples antiques qui se rapprochaient le plus de la « vraie année », grâce à leurs compétences en mathématiques. Le système de Numération Égyptienne était également utilisé avec d’excellents résultats pour construire des tombes, des pyramides et autres merveilles architecturales.

La Numération Égyptienne et l’architecture de la Grande Pyramide

La Grande Pyramide de Khéops de la quatrième dynastie était une merveille de mathématiques : elle était disposée avec une précision géométrique – une base carrée presque parfaite, avec des côtés de 230 mètres qui diffèrent les uns des autres de moins de 20 centimètres, et des faces qui s’inclinaient vers le haut à un angle de 51 pour atteindre un sommet à près de 150 mètres au-dessus du sol du désert.

La pyramide compte environ 2 300 000 blocs de pierre géants et lourds, qui sont placés si près les uns des autres qu’il est impossible d’insérer une lame de couteau entre deux ! Les côtés de la base carrée ont une erreur de moins de 1/14 000, tandis que les angles droits ont une erreur de moins de 1/27 000.

Les chercheurs ont fait de nombreuses découvertes sur la Grande Pyramide en utilisant les mathématiques :

En utilisant la coudée égyptienne, le périmètre est de 365,24 – le nombre de jours de l’année ;
L’inclinaison de l’apex à la base est égale au 600^ème d’un degré de latitude ;
La hauteur multipliée par 10 puissance 9 donne approximativement la distance de la terre au soleil ;
Le périmètre divisé par 2 multiplié par la hauteur de la pyramide est égal au nombre pi : 3,1416 ;
Le poids de la pyramide x 10 puissance 15 est égal au poids approximatif de la terre ;
Lorsque les diagonales croisées de la base sont additionnées, le résultat est égal au temps (en années) qu’il faut pour que l’axe polaire de la terre revienne à son point de départ initial : 25 286,6 ans ;
Les mesures de la Chambre du Roi donnent 2-5-3 et 3-4-5, qui sont les triangles de base de Pythagore

En manipulant les chiffres, on peut tout prouver, il faut donc prendre tout cela avec des pincettes… Ce que les Égyptiens ont réalisé à l’aide de leur système mathématique qui, nous l’avons vu, était peu maniable, fut en fait assez fantastique. Non seulement ils l’ont utilisé dans leur vie quotidienne, mais ils ont aussi construit l’une des sept merveilles du Monde antique. Quelque chose que nous, aujourd’hui, ne saurions pas reproduire malgré nos connaissances bien plus avancées en mathématiques et notre technologie moderne !

Vous pouvez aussi lire notre article sur la signification du chiffre 222.